线性的递归和迭代

n! 就是等于 n乘(n-1)!

scheme:

1
2
3
4
(define (factorial n)
  (if (= n 1)
      1
      (* n (factorial (- n 1)))))

另一种方式
先乘1和2，将结果乘3，再乘4。
我们要维持一个变化的乘积product，以及一个从1到n的计数counter。

product <- counter * product
counter <- counter + 1

scheme:

1
2
3
4
5
6
7
8
9
(define (factorial n)
  (fact-iter 1 1 n))

(define (fact-iter product counter max-count)
  (if (> counter max-count)
      product
      (fact-iter (* product counter)
                 (+ counter 1)
                 max-count)))

树形递归

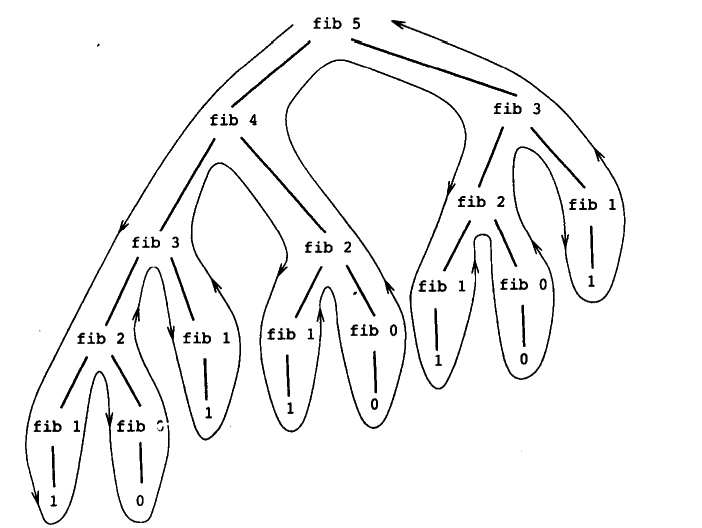
每一个数都是前两个数之和。

缺点：存在重复，fib 3差不多是这里一半的工作，这个计算过程重复做了两次。

求幂

对一个给定数进行求幂运算，参数是一个基数b，和一个正整数的指数n。

scheme：

1
2
3
4
(define (expt b n)
  (if (= n 0)
      1
      (* b (expt b (- n 1)))))

转换成线性迭代形式：

1
2
3
4
5
6
(define (expt-iter b counter product)
  (if (= counter 0)
      product
      (expt-iter b
                 (- counter 1)
                 (* b product))))