记录学习的知识点。

程序设计的基本元素

  1. 基本表达形式，最简单的个体。
  2. 组合的方法，从简单的东西出发构造出复合的元素。
  3. 抽象的方法，为复合对象命名，并将他们当做单元去操作。

表达式

234 ，就是一个数，它也是一个表示数的表达式。
+ - * / ,这些运算符，属于表示过程的表达式，比如表示加的过程，表示减的过程。
将这两个组合，就形成了复合表达式。表示把加减乘除的过程应用到这些数上。

1
2
(+ 112 342)
454

命名

我有一个数字3.14，我给它取一个名字叫pi，这个名字就叫变量，它的值就是3.14。

scheme里用define方式完成:

1
2
3
> (define pi 3.14)
> pi
3.14

define它允许我们用一个简单的名字去引用一个组合运算的结果.

1
2
3
> (define sum (+ 2 2))
> sum
4

环境

我们将3.14和pi这个名字用define定义好，后面又可以通过pi获取到3.14，那么解释器显然有存储能力，存储了pi和3.14的关系，这种存储就叫环境。

环境所扮演的角色就是确定名字（符号）的意义。

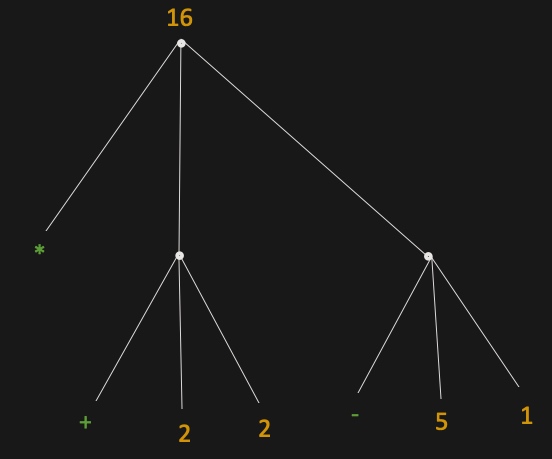
组合式求值

1
2
(* (+ 2 2)
    (- 5 1))

这就是一个组合式，它是由若干个表达式组成的。
对它求值要做下面的事情：

  1. 对它的子表达式们进行求值，求值(+ 2 2)得到值4，求值(- 5 1)得到值4。
  2. 将最左边的运算符的过程应用到这两个值上，形成(* 4 4)。这两个值属于该表达式的参数。

为了实现对组合式的求值，我们必须先对组合式里的每一个元素做同样的求值过程。在性质上，这一求值过程是递归的。

用树状结构表示：

复合过程

1
(define (square x) (* x x))

这个复合过程，表示将一个东西乘它自己。这个东西也给它取个名字叫x。
然后我们再将整个复合过程取一个名字叫square。

定义好后，就可以调用它了。

1
2
> (square 10)
100

我们还能将square当做基本构件去定义其他过程。

1
2
3
4
5
> (define (sum-of-squares x y)
  (+ (square x) (square y)))
  
> (sum-of-squares 3 4)
25

代换模型

1
2
(define (f a)
  (sum-of-squares (+ a 1) (* a 2)))

说白了就是将形参换成实参，比如将a换成5。

1
(f 5)

提取出f的体。

1
(sum-of-squares (+ a 1) (* a 2))

用实际的参数5替换其中的形式参数。

1
(sum-of-squares (+ 5 1) (* 5 2))

现在运算符是sum-of-squares，两个运算对象分别是(+ 5 1)和(* 5 2)。
我们必须对运算符求值，得到那个过程。还需要对两个对象进行求值。
两个对象分别是5和10，用它们替换掉sum-of-squares过程中参数x和y

1
(+ (square 6) (square 10))

square又可以进一步约分为：

1
(+ (* 6 6) (* 10 10))

通过乘法又能将它们约分为:

1
(+ 36 100)

最后得到

1
136

应用序和正则序

正则序的求值方法和上一章不同，而是先不求出对象的值，等用到它们的之后再去做。

1
2
3
(sum-of-squares (+ 5 1) (* 5 2))
(+  (square (+ 5 1))    (square (* 5 2)))
(+  (* (+ 5 1) (+ 5 1))   (* (* 5 2) (* 5 2 )))

然后才是约分：

1
2
3
(+  (* 6 6)   (* 10 10))
(+    36           100)
            136

与正则序对应的是现在解释器里用的，”先求值参数而后应用”的方式，它被称为应用序求值。

条件表达式

至此我们定义出的过程表达能力还非常有限，还没有办法根据某种结果去做不同的操作。

这种结构称为分情况分析，检查一个数是正负或者0，根据不同的情况采取不同的动作。
Lisp中有着针对该情况的特殊形式，称为cond:

1
2
3
4
(define (abs x)
  (cond ((> x 0) x)
        ((= x 0) 0)
        ((< x 0) (- x))))

它表示如果 (> x 0)的条件为false，那就去求下一个(= x 0)，如果还是false那就以此类推，知道发现那个条件为True的为止。
如果无法找到为True的条件，cond的值就没有定义。

还有一种写法是：

1
2
3
(define (abs x)
  (cond ((< x 0) (- x))
        (else x)))

如果x小于0就返回-x，否则就返回x。

还有一种写法：

1
2
3
4
(define (abs x)
  (if (< x 0)
      (- x)
      x)

这里采用的是if形式。

逻辑复合运算符

and表达式：

1
2
3
4
> (and 1 1)
1
> (and 1 0)
0

or表达式：

1
2
3
4
> (or 1 1)
1
> (or 1 0)
1

not表达式: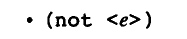

如果是True，就返回False
如果是False，就返回True。

1
2
3
4
> (not #t)
#f
> (not #f)
#t

定义一个大于等于的过程:

1
2
(define (>= x y)
  (or (> x y) (= x y)))